Generative Adversarial Networks (GANs) are generative machine learning models that solve the problem of generating new data from the probability space of the training data instead of simply classification and regression.

GANs consist of two neural networks that compete against one another in a zero-sum game. The two networks are called Generator and Discriminator and their functions are as follows

Generator

The task of the generator is to create new data points that resemble closely with the data points of the training data. The generator should be able to generate new points that appear as if they have been sampled from the original distribution. The generator typically takes input from the latent space and generates a data point in the space of training data. The input to the network is a point in latent space that is sampled randomly. The generator typically has deconvolution layers for converting the latent representations into original representations (such as images). The generator tries to increase the loss of the discriminator by fooling discriminator into believing that the data point generated belongs in the original space.

Discriminator

The task of the discriminator is to successfully distinguish between real samples and those generated by the generator. Since this is a classification task, discriminators are typically convolutional neural networks that try to classify the input data point into real and artificially created samples. The loss of discriminator is typically a cross entropy loss for classification. The discriminator tries to increase the loss of the generator by successfully discriminating the samples artificially created by the generator. The generator and the discriminator play a minimax game with the following function

$$\displaystyle \min\limits_G\max\limits_D V(D, G) = {\mathbb E}_{x\sim p_{\rm data}(x)}[\log D(x)]+{\mathbb E}_{x\sim p_z(z)}[\log (1-D(G(z)))]$$

This function is simple to understand.

$D(x)$ represents the probability that x came from the probability distribution of the training set (according to the discriminator).

$G(z)$ represents the output of the generator on the latent vector z.

If this function ($V(G, D)$) has a high value then -

1. The first term calculates the expectation of log probability that the data point sampled from the training dataset has a high probability of being predicted as sampled from training data by the discriminator.
2. The second term is calculated over the probability distribution of the noise vectors that is used by the input of the generator for generating new points. It is the expectation that this noise vector z, when converted into a data point by the generator (i.e. $G(z)$) has a very low probability of being classified as from the original training data space.

So, the discriminator tries to increase this function since then, it would be able to better distinguish between data from the original space of training data and the generator tries to decrease it so that, the discriminator can’t distinguish between the real and the synthesized examples. Since, the only variable for the generator is the $G(z)$, generator can only change itself and not the discriminator function (i.e. it can’t reduce the discriminator’s ability to distinguish). Similarly, the discriminator can only change the function $D$ and not $G(z)$. So, discriminator can’t reduce the generator’s ability to produce good output.

So, both compete against one another and both try to improve themselves rather than making the other worse and so, both acquire a good ability to perform the tasks assigned to them.

Algorithm

• for number of training iterations do
  • for k steps do
    • Sample minibatch of m noise samples ${z^{(1)}, \ldots, z^{(m)}}$ from noise prior $p_g(z)$.
    • Sample minibatch of m examples ${x^{(1)}, \ldots x^{(m)}}$ from data generating distribution $p_{\rm data}(x)$.
    • Update the discriminator by ascending its stochastic gradient: $\displaystyle\nabla_{\theta_d}\frac 1m\sum_{i=1}^m\left[\log D(x^{(i)})+\log(1-D(G(z^{(i)})))\right]$
  • end for
  • Sample minibatch of m noise samples ${z^{(1)}, \ldots, z^{(m)}}$ from noise prior $p_g(z)$.
  • Update the generator by descending its stochastic gradient: $\displaystyle\nabla_{\theta_g}\frac 1m\sum_{i=1}^m\left(1-D(G(z^{(i)}))\right)$
• end for

Typical architecture of Generator (for image synthesis)

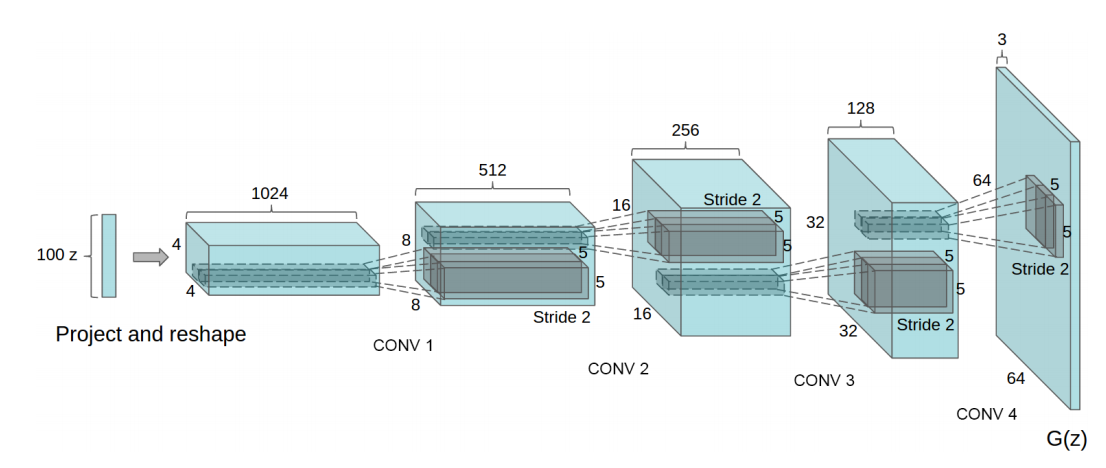
The noisy input is deconvoluted to form the final image.

Experiments

We experimented on the MNIST dataset for handwritten digits. We observed the results as shown in figure. The code can be found in the Code folder.

Problems associated with GANs

Other than general problems associated with machine learning models such as overfitting and hyperparameter selection, GANs have several other problems associated with them. Some of them are as follows

• Non-Convergence : The model parameters never converge to an optimum under some settings and keep oscillating.
• Mode Collapse : The generator always produces the same or very similar output irrespective of the input.
• Diminished : The discriminator might become very strong at distinguishing. In that case, the gradient of the generator might become negligible and so, it might stop learning.
• Non-Semantic Vectors : The latent space vectors are sampled from a prior probability distribution. So, there is no way for semantically deciding the type of images required. For generating a particular type of image (in an unsupervised setting), all posibile latent space vectors might need to be looked at. InfoGANs provide a way for encoding these semantic features in addition to the random vector for generating images with certain properties (such as specific stroke thickness in case of MNIST dataset images).

References

• Goodfellow, Ian, et al. “Generative adversarial nets.” Advances in neural information processing systems. 2014.