DCGANs are a variation of GANs. The problem they try to resolve is -
Problem with GANs that DCGANs try to resolve
If the vanilla GANs use only fully connected layers for generating as well as discriminating, then the final output may not support the localization property of images (i.e. similar information occurs together). This could lead to random pixels disconnected from the actual object.
Also, if the localization property isn’t exploited, then a larger number of weights have to be learned when compared with a convolutional architecture of similar size (since CNNs have lesser number of weights for the same amount of layers due to their exploitation of spatial locality). This means, for images, CNN based GANs would yield better results since more number of layers can be trained on the same architecture due to this exploitation of locality.
However, a major problem with CNN based GANs is that they are very unstable, i.e. the weights might keep oscillating for a lot of different values of hyperparameters. This variant offers some basic design techniques for the construction of CNN based GANs that lead to convergence under a lot of different scenarios.
So, DCGANs (Deep Convolutional Generative Adversarial Networks) solve the problem of non-convergance to a certain extent.
Approach
DCGANs provide the following general guidelines for constructing the CNN based GANs -
-
Replace any pooling layers with strided convolutions in discriminator and fractional-strided convolutions in the genertor.
The rationale behind this is that this gives the network ability to generalize downscaling operations. Pooling operations (such as max pooling) is one specific type of downsampling. The network can now learn its own pooling operation.
-
Using batchnorm in both discriminator and generator.
The idea behind this is that, the paper recommends the use of relu based activations throughout the network. However, in the last layer of both the generator and discriminator, tanh or sigmoid based activations have to be used (to confine the results to a particular range). Confining to a range is required because the image pixels must have a pre-defined range and the discriminator output must be a confidence score (say, from 0 to 1). However, these non-linearities are extremely sensitive to inputs.
If the inputs to these non-linearities are either too positive (the output of Relu layers will likely have high positive value) or too negative, then tanh and sigmoid will saturate right in the beginning and would never learn anything. So, to avoid this saturation, a batch normalization has to be done so that the mean is close to 0 and variance is close to 1.
-
Remove fully connected hidden layers for deeper architectures.
The idea here is that in several state of the art image classification models, global average pooling is used instead of fully connected layers to directly compute a global average of each activation map. Global average pooling tends to increase network stability but, could hurt convergence speed. So, instead, the output of the last convolutional layer is fed directly into the output of the discriminator and similarly, the input (i.e. noise) of the generator is directly fed in the first convolutional layer of the generator.
-
Use ReLU activation for all layers in generator except for the last which uses tanh.
The idea is very simple. Using bounded non-linearities such as tanh and sigmoid in hidden layer neurons leads to quick saturation of neurons. However, the last layer of the generator has to be a bounded non-linearity since the image pixel intensities can vary in a bounded range only.
-
Use LeakyReLU activation for all layers in discriminator.
Empirically, it was observed that LeakyReLU led to better results especially for getting higher resolution images.
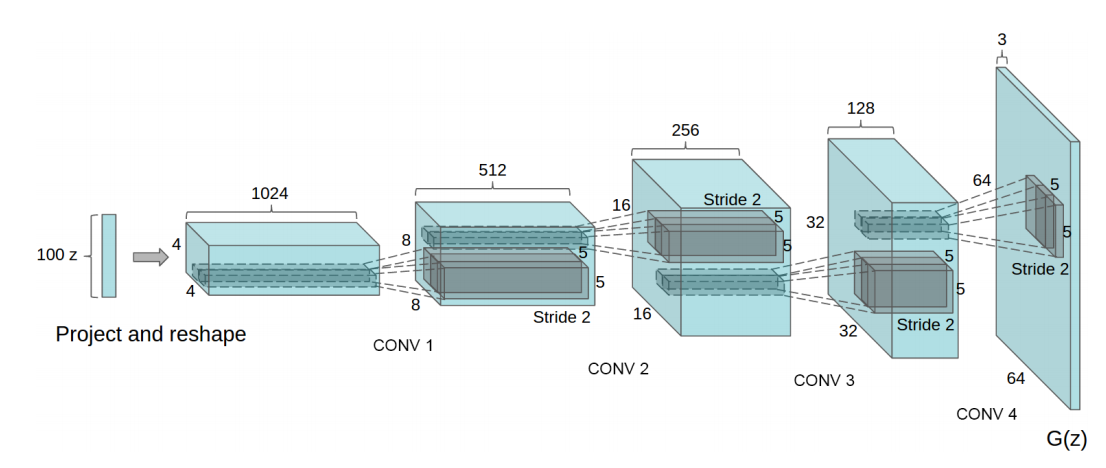
A model generator architecture is shown in the figure.
Empirically, it was observed that with learning rate 0.0002 and $\beta_1$ = 0.5 in Adam optimizer, instability was reduced even further.
Experiments
- (From paper) A model was trained on the LSUN bedrooms dataset containing 3 million examples. To verify that the model hasn’t memorized the training examples, interpolation was done on 9 random points in the latent space. It was observed that all the images generated represent a plausible bedroom with a smooth transition. This suggests that the model hasn’t memorized the examples, but instead has discovered the relevant features for the creation of the relevant images.

- (From code) We experimented on the MNIST dataset for handwritten digits. We observed the results as shown in figure. The code can be found in the Code folder.

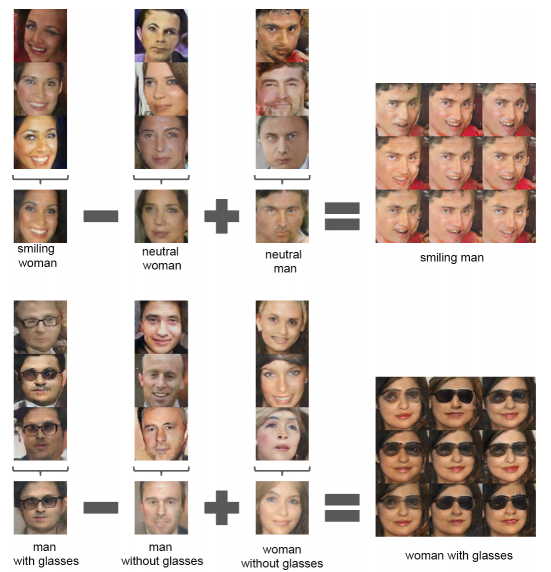
Face Arithmatic
Another interesting approach presented in this paper was the arithmetic on the latent space. A single model was trained for generating faces of people. The images generated by the model were then manually classified into categories such as “smiling women”, “neutral women” and “neutral man”.
Three vectors in the latent space corresponding to each category (i.e. those latent vectors that created particular images of each class) were picked and averaged. Then, on the averaged latent space vectors, arithmatic was performed. It was observed that when this final latent vector was fed into the generator, the output image corresponded to the expected output category (i.e. “smiling man”). This suggests that the latent vectors contain the relevant features for such arithmetic to work. This shows that the representations learned by the network have semantic meaning as well.