In traditional GANs the data is unconditionally generated but we can condition the model on additional information which can direct the data generation process.

Conditional Adversarial Nets

GANs

For GANs we have the value function:

$$\min\limits_G\max\limits_D V(G, D)={\mathbb E}_{x\sim p_{\rm data}}[\log D(x)]+{\mathbb E}_{x\sim p_z}[\log(1-D(G(z)))]$$

cGANs

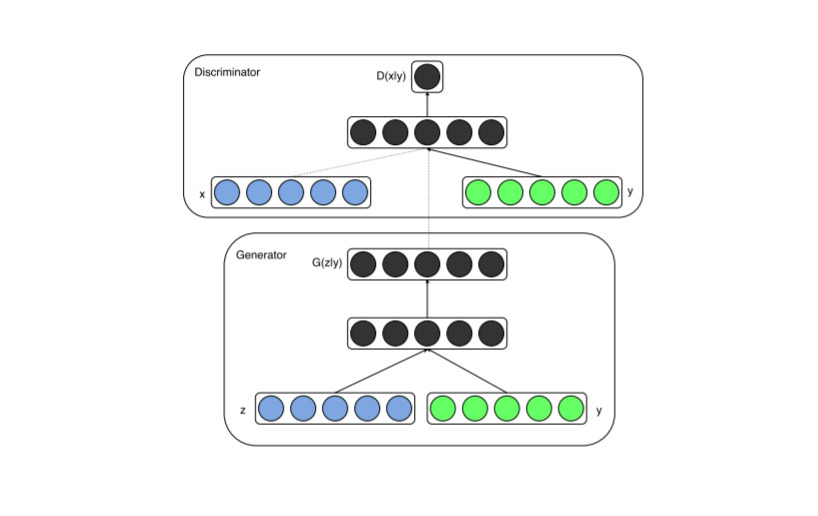
We can extend GANs to include some extra information $y$ which can be any auxiliary information such as cass labels or data from other madlities. We can perform conditioning by feeding $y$ into both the discriminator and generator as additional input layer.

• In generator the prior input noise $p_z(z)$ and $y$ are combined in joint hidden representation.
• In the discriminator $x$ and $y$ are presented as inputs.

The objective function becomes:

$$\min\limits_G\max\limits_DV(G, D)={\mathbb E}_{x\sim p_{\rm data}}[\log D(x\mid y)]+{\mathbb E}_{x\sim p_z(z)}[\log(1-D(G(z\mid y)))]$$

This is illustrated in the below figure:

Experiments

1. Generator: (From paper) We trained a conditional adversarial net on MNIST images conditioned on their class labels encoded as one-hot vectors. Noise prior $z$ with dimensionality $100$ was drawn from a normal distribution. Both $z$ and $y$ are mapped to hidden layers with ReLu activation with layer sizes $200$ and $1000$ respectively, before both being mapped to second, combined hidden ReLu layer of dimensionality $1200$. We have a final tanh unit layer as our output for generating the $784$-dimensional MNIST samples.
2. Discriminator: (From paper) The discriminator maps $x$ to a max-out layer with $240$ units and $5$ pieces, and $y$ to a max-out layer with $50$ units and $5$ pieces. Both the hidden layers are mapped to joint max-out layer with $240$ units and $4$ pieces before being fed to a sigmoid layer.
3. Model: (From code) The model was trained using Adam with learning rate $\eta=0.0002$ and $\beta_1=0.5$
4. (From code) We experimented on the MNIST dataset for handwritten digits. We observed the results as shown in figure. The code can be found in the Code folder.

References

• Mirza, Mehdi, and Simon Osindero. “Conditional generative adversarial nets.” arXiv preprint arXiv:1411.1784 (2014).